Quicksort Algorithm

The quicksort algorithm is similar to merge sort in that it takes the same divide and conquer approach that the merge sort algorithm uses. Quicksort works by partitioning an array into two sub-arrays. Merge sort does the same thing, but quick sort does it by seperating the partition around a pivot point. The numbers less than the pivot point are placed into the lower array and those above into a higher array. The function then runs recursively continuing to sort the arrays until they are seperated into fully sorted arrays. The array ends completly sorted and merged back into one array. Quick sort is normally extremely fast in practice, although its worst case scenario running time is O(n^2), but the average case is O(n*logn^2) making it the fastest of the five sorting algorithims looked at.

Merge Sort

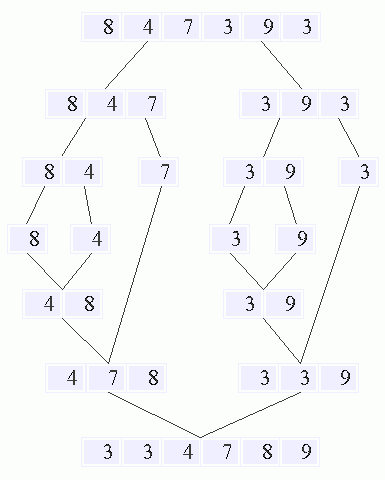
Merge Sort is a more advanced sorting algorithm it is more complex to code, understand, and implement, but it also provides a more efficient algorithm. The merge sort algorithm works by dividing the array into separate arrays and then sorting the smaller arrays and then eventually merging the arrays back together sorted. The sorting is done by recursive calls to the merge sort function. The array is divided as many times as it takes in order to get an array with only one element. Once an array with one element is reached the arrays are then placed back together with each array being put back in the proper order through recursive calls to the merge sort function. After each array has been sorted it a call to the function merge places it back into one array properly sequence by keeping track of the smallest element in each array and inserting the smaller of the two until every element has been placed back into the original array. The advantages that merger sort brings is that it has a time complexity of O(nlogn) as compared to O(n^2) of the other three algorithms looked at so far.

Insertion Sort

Insertion sort is the third sorting algorithm that I will be explaining how it works as well as the advantages and disadvantages of its use. The idea of insertion sort is partitioning the array into a sorted and unsorted sections. Then you insert each element from the unsorted partition into its proper place in the sorted partition. This is easily accomplished by starting the sorter partition with only one element, the first element in the array, the other side will have n-1 elements. The algorithm will continue until eventually the sorted side will have n-1 elements and the unsorted side will have n elements. Then the last element is properly placed into the sorted section and the array has successfully been sorted. The advantages of of insertion sort is that it can be quicker than the other algorithms because it takes into account partially sorted arrays. The only problem is it is still not a very efficient algorithm because when the list is in the reverse order it will end up the same running time as the other two algorithms at big Oh (n^2).

Bubble Sort

Bubble sort is another sorting algorithm which can easily be implemented using C++ and other programming languages. The idea behind the bubble sorting algorithm is that you compare two elements which are adjacent to one another and exchange the elements if the larger one is not in the proper order. With each pass of the array the element becomes more and more sorted and eventually can sort the array into either ascending or descending order. An example of a few passes of a bubble sort algorithm is provided below.

Pass 1

21 15 43 10 23
15 21 43 10 23
15 21 10 43 23
15 21 10 23 43

Pass 2

15 21 10 23 43
15 10 21 23 43

Pass 3

15 10 21 23 43
10 15 21 23 43

Again the bubble sort algorithm is simple to understand and easy to implement. The disadvantages of bubble sort algorithm is that they can often have long running times due to a large time complexity and the need for many passes of through the entire array.

Selection Sort

Selection sort is a relatively simple sorting algorithm. It can be used to sort the data elements within an array. To explain the algorithm I will refer to an array called array A, which contains n number of elements of a particular data type. To make the example easier to explain assume that it contains unsorted integer numbers. In order to get the array in the correct order you need to find the index of the largest element within the array. Once that number has been located it can then be swapped with the last index within the array. The algorithm then will run through the array again taking the next largest integer and swapping it into the index of [n-2]. This process will continue until the index of A[0] is reached. Below I have provided a trace of the selection sort algorithm.

Original Array: 29 10 14 37 13

After 1st swap: 29 10 14 13 37
After 2nd swap: 1310 14 29 37
After 3rd swap: 13 10 14 29 37
After 4th swap: 10 13 14 29 37

The selection sort algorithm is a simple algorithm to implement, but at times can have a relatively large time complexity. It also is an internal sorting algorithm which requires it to all be able to fit in primary memory.

Sorting Algorithms

Sorting is the process of taking data and arranging it into either ascending or descending order. It is a very common process that is utilized often in computer programming. There are two categories of sorting, internal sorts or external sorts. An internal sort requires that the entire collection of data fits inside the computers main memory. An external sort requires that the data would have to be stored in secondary memory. The memory of a computer is divided into either the primary memory or secondary memory. Secondary memory would be held on the hard drive, while the primary memory is on the CPU itself. Internal sorts are able to be performed at a quicker rate than the external sort. Through the next several posts I will be looking at specific sorting algorithms and how each is implemented. There are certain assumptions that need to be made in order to understand the algorithm. The algorithm will be passed an array n elements of type int, and those will be sorted into ascending order.

C++ Standard Template Libraries

Many people are surprised to realize that they do not always have to write all the code for everything they are trying to do. Many data structures and commonly used functions are already written and stored in templates online. Those for C++ can be found here. The templates on the website contain the basic codes for common data structures like lists, vectors, stacks, queues and several other basic structures. The codes are categorized and easy to locate. The codes provided are the basics for the particular data structure and can then be modified to accomplish what it is that you need the code to do in particular. It is a very useful resource which allows to drastically cut down programming time. Most other computer programming languages have similar sites which contain codes for structures in those languages.